Ako vypočítať sklon strechy?

Sklon strechy je vyjadrený ako uhol strešnej roviny, ktorý táto zviera s vodorovnou rovinou, pričom sa vyjadruje v stupňoch, prípadne v percentách. Prečo je dôležité poznať sklon strechy? Ako vypočítať sklon strechy? Čo všetko závisí od sklonu strechy? Na tieto otázky vám prinášame odpovede v nasledujúcich riadkoch.

Prečo je dôležité poznať sklon strechy?

Strešná krytina šikmej strechy sa považuje za bezpečnú, ak zamedzuje vnikaniu zrážkovej vody (dážď, sneh, roztopený sneh a pod.) do podstrešného priestoru. Sústava dômyselne navrhnutých vodných drážok na jednotlivých škridlách zabezpečuje odtok vody z vyššie položených škridiel na nižšie umiestnené. V normálnych podmienkach je teda všetka voda bezpečne odvedená zo strešnej roviny do odkvapového systému a odtiaľ na zem, resp. do kanalizačného systému. V prípade abnormálnych poveternostných javov sa určité množstvo vody môže dostať pod krytinu. V tomto prípade sa svojej úlohy ujme poistná hydroizolácia, ktorá časť zrážkových vôd vyskytujúcich sa pod strešnou krytinou bezpečne odvedie a podstrešný priestor ostane opäť suchý.

V prípade plochých striech je situácia iná. Tie musia byť vodotesné po celej svojej ploche. Jednotlivé pásy tvoriace strešnú krytinu vytvárajú súvislú membránu, teda povlak, ktorý je úplne uzatvorený.

Práve správny odvod vody zo strechy je jedným z hlavných dôvodov, prečo je nutné poznať sklon strechy. Okrem toho sklon strechy ovplyvňuje napríklad aj výber strešnej krytiny a jej kotvenie a latovanie, ako aj využiteľnosť podkrovia a estetický vzhľad budovy.

Čo všetko závisí od sklonu strechy?

Každá strešná krytina má deklarovaný špecifický hraničný sklon strechy. Je to najnižší uhol sklonu, pri ktorom sa daná krytina osvedčila ako odolná voči vnikaniu zrážkovej vody. Ide o minimálny uhol, pre ktorý je krytina vyhovujúca, preto by reálny sklon strechy mal byť väčší, ako je predpísaná hraničná hodnota.

Vo všeobecnosti platí, že čím vyššie sú drážky slúžiace na odvod vody na konkrétnom druhu krytiny alebo čím väčšie je jej výškové prekrytie, tým viac sa jej hraničný sklon posúva k nižším hodnotám. Tie sa v prípade tvrdých skladaných krytín začínajú na hodnote 22°. (Na trhu sú aj krytiny špecifického tvaru určené na nižšie sklony striech, no je nutné použiť tzv. vodotesné podstrešie, ktoré realizáciu strechy predražuje.) Uhol sklonu strechy 30° je potom bezpečný už pre väčšinu krytín.

Od uhla sklonu strešnej roviny závisí aj potreba kotvenia škridiel umiestnených na strešnej rovine. Pri sklone nad 45° je dôležité kotviť každú tretiu škridlu na ploche a pri sklone nad 60° je nutné kotviť už každú škridlu, a to skrutkou alebo klincom cez predvŕtaný otvor v škridle, prípadne špeciálnou príchytkou.

Pripomíname, že bez ohľadu na sklon strechy je nutné kotviť aj:

• každú okrajovú škridlu pri štíte, každú tretiu škridlu pri odkvapovej hrane, každý hrebenáč, každú škridlu na pultovej hrane,
• všetky rezané škridly na nárožiach alebo úžľabiach a všetky okrajové škridly,
• škridly potrebné na záveternej strane strechy pod hrebeňom, keďže v tejto oblasti dochádza k sacím účinkom vetra a neprichytené škridly môžu byť pri silnom vetre zo strechy vytrhnuté.

Uhol sklonu strechy má vplyv aj na návrh rozstupu latovania a výšky, resp. plochy vetracej medzery pod krytinou. Ovplyvňuje skladbu strešného plášťa, spôsob upevnenia škridiel na ploche strechy, ale aj návrh protisnehových opatrení.

Zdá sa vám to príliš zložité? Nezúfajte. Dobrý strechársky majster by mal mať tieto informácie v malíčku a mal by ich aj uplatňovať.

Ako vypočítať sklon strechy? Potrebné rozmery

Vráťme sa však k samotnému výpočtu sklonu strechy. Ak budete chcieť vypočítať, aký sklon má vaša strecha, budete na to potrebovať poznať dva rozmery strechy, ktoré obvykle nie je problém odmerať. Bude to výškový rozdiel medzi odkvapom a hrebeňom, inak povedané výška strechy. Tento rozmer označíme ako V. Ďalší rozmer, ktorý bude nutné odmerať, je pôdorysná vzdialenosť medzi odkvapom a hrebeňom. Označíme ju ako A. Následne sa môžeme pustiť do výpočtu sklonu strechy v percentách alebo stupňoch.

V ojedinelých prípadoch sa vám môže stať, že nebudete schopní zmerať výšku strechy. Vtedy prichádza do úvahy výpočet sklonu strechy pomocou dvoch rozmerov, a to prostredníctvom dĺžky krokvy (označíme ju ako K) a už spomenutej pôdorysnej vzdialenosti medzi odkvapom a hrebeňom (A).

Skôr než sa pustíte do výpočtov pomocou vzorcov

Ak neradi počítate, sú aj jednoduché riešenia, ako zistiť sklon strechy. Môžete použiť sklonomer, mobilné aplikácie alebo kalkulátor na výpočet sklonu strechy, do ktorého len zadáte vyššie zmienené základné rozmery a výsledok máte okamžite k dispozícii.

V prípade, že si chcete výpočet spraviť sami, nižšie si uvedieme možnosti.

Ako vypočítať sklon strechy v percentách?

Ak vydelíte rozmer V (v centimetroch) a rozmer A (v metroch), získate sklon strechy v percentách (%).

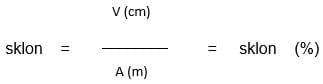
Príklad:
Meraním sme zistili, že strecha má výšku (V) 450 cm a pôdorysná vzdialenosť odkvapu od hrebeňa (A) je 7,5 m.

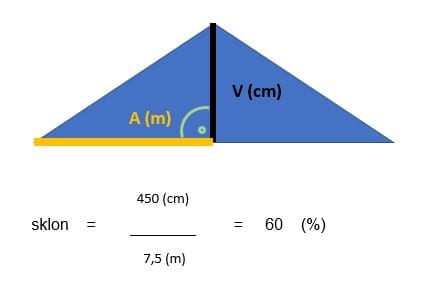
Odpoveď:
Z nameraných hodnôt pre výšku (V) 450 cm a pôdorysnú vzdialenosť odkvapu od hrebeňa (A) 7,5 m sme vypočítali sklon strechy, ktorý sa rovná 60 %.

Ako vypočítať sklon strechy v stupňoch?

Ak budeme chcieť v takomto prípade vypočítať uhol sklonu strechy v stupňoch, musíme si vziať na pomoc goniometrickú funkciu tangens.

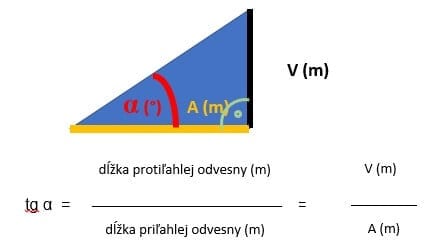
Príklad:
Meraním sme zistili, že strecha má výšku (V) 4,5 m a pôdorysná vzdialenosť odkvapu od hrebeňa (A) je 7,5 m.

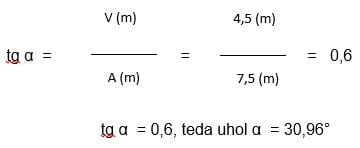
Odpoveď:
Z nameraných hodnôt pre výšku (V) 4,5 m a pôdorysnú vzdialenosť odkvapu od hrebeňa (A) 7,5 m sme vypočítali uhol sklonu strechy, ktorý sa rovná 30,96°.

Poznámka: Z uvedených príkladov vyplýva, že sklonu strechy 60 % zodpovedá uhol sklonu 30,96°.

Upozorňujeme, že na základe tejto metodiky sklonu 100 % zodpovedá uhol sklonu strešnej roviny 45°. Nie je teda nič neobvyklé, ak pri strmších strechách budeme pracovať so sklonom väčším ako 100 %.

Ako previesť hodnotu tangens na stupne?

Vzhľadom na to, že pomocou bežne dostupných kalkulačiek je dnes prevod goniometrickej funkcie tangens na uhol mierne zložitejší a nie každý má doma matematické tabuľky, uvádzame pomocné tabuľky.

Tab. 1: Pomocná tabuľka slúžiaca na prevod sklonu v percentách na sklon v stupňoch

Sklon v percentách (%)	Sklon v stupňoch (°)
5	2,86
10	5,71
15	8,53
20	11,31
25	14,04
30	16,7
35	19,29
40	21,8
45	24,23
50	26,57
55	28,81
60	30,96
100	45

Tab. 2: Pomocná tabuľka slúžiaca na prevod hodnoty tg α na uhol α

α	tg α	α	tg α	α	tg α
0	0,0000	30	0,5774	60	1,7321
1	0,0175	31	0,6009	61	1,8040
2	0,0349	32	0,6249	62	1,8807
3	0,0524	33	0,6494	63	1,9626
4	0,0699	34	0,6745	64	2,0503
5	0,0875	35	0,7002	65	2,1445
6	0,1051	36	0,7265	66	2,2460
7	0,1228	37	0,7536	67	2,3559
8	0,1405	38	0,7813	68	2,4751
9	0,1584	39	0,8098	69	2,6051
10	0,1763	40	0,8391	70	2,7475
11	0,1944	41	0,8693	71	2,9042
12	0,2126	42	0,9004	72	3,0777
13	0,2309	43	0,9325	73	3,2709
14	0,2493	44	0,9657	74	3,4874
15	0,2679	45	1,0000	75	3,7321
16	0,2867	46	1,0355	76	4,0108
17	0,3057	47	1,0724	77	4,3315
18	0,3249	48	1,1106	78	4,7046
19	0,3443	49	1,1504	79	5,1446
20	0,3640	50	1,1918	80	5,6713
21	0,3839	51	1,2349	81	6,3138
22	0,4040	52	1,2799	82	7,1154
23	0,4245	53	1,3270	83	8,1443
24	0,4452	54	1,3764	84	9,5144
25	0,4663	55	1,4281	85	11,4301
26	0,4877	56	1,4826	86	14,3007
27	0,5095	57	1,5399	87	19,0811
28	0,5317	58	1,6003	88	28,6363
29	0,5543	59	1,6643	89	57,2900

Ak máte k dispozícii vedeckú kalkulačku, budete si môcť vypočítať uhol sklonu strechy v stupňoch, a to pomocou goniometrickej funkcie tangens a jej inverznej funkcie arkustangens.

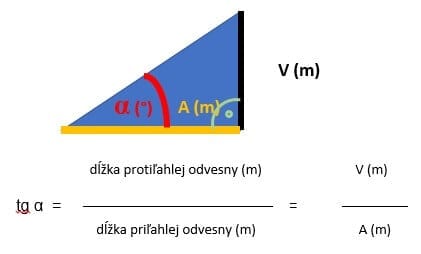
Keďže zároveň platí, že arctg (tg α) = α, potom uhol α vypočítate pomocou vedeckej kalkulačky stlačením tlačidla 2ndF alebo INV a tan.

Príklad:
Meraním sme zistili, že strecha má výšku (V) 4,5 m a pôdorysná vzdialenosť odkvapu od hrebeňa (A) je 7,5 m.

arctg (tg α) = α

Odpoveď:

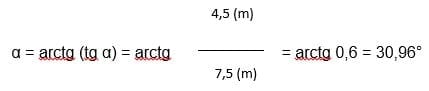
Z nameraných hodnôt pre výšku (V) 4,5 m a pôdorysnú vzdialenosť odkvapu od hrebeňa (A) 7,5 m sme vypočítali uhol sklonu strechy, ktorý sa rovná 30,96°.

Ako vypočítať sklon strechy pri poznaní dĺžky krokvy?

V ojedinelých prípadoch sa vám môže stať, že nebudete schopní zmerať výšku strechy. Pri troche šťastia a určitom fyzickom úsilí sa vám podarí odmerať dĺžku krokvy. Označíme ju ako K. Ďalším rozmerom, ktorý budete potrebovať odmerať, je – ako v predošlých prípadoch – pôdorysná vzdialenosť medzi odkvapom a hrebeňom. Označíme ju ako A.

V takom prípade bude situácia takáto:

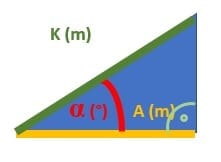
Pomôžeme si znalosťou funkcie kosínus:

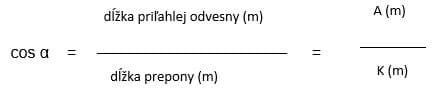
Keďže zároveň platí, že arccos (cos α) = α, potom uhol α vypočítate pomocou vedeckej kalkulačky stlačením tlačidla 2ndF alebo INV a cos.

Príklad:

Meraním sme zistili, že strecha má dĺžku krokvy (K) 8,75 m a pôdorysná vzdialenosť odkvapu od hrebeňa (A) je 7,5 m.

Odpoveď:

Z nameraných hodnôt pre dĺžku krokvy (K) 8,75 m a pôdorysnú vzdialenosť odkvapu od hrebeňa (A) 7,5 m sme vypočítali uhol sklonu strechy, ktorý sa rovná 31°.